
Actividad 7
ACTIVIDAD 7-GRAFOS
Introducción a grafos de JAVIER OSPINA MORENO
Actividad:
1. Definir que es un grafo
2. ¿Que uso se le dan a los grafos?
3. ¿Como se pueden clasificar los grafos?
4. ¿Como se pueden representar los grafos?
Nota: Recuerde que cada pregunta debe ir acompañada de:
- Los enlaces de donde consulto la información (normas Apa) .
- De un aporte personal con sus propias palabras de lo que entendió de lo consultado.
- De una imagen que tenga relación con el tema o pregunta con su respectivo enlace (normas Apa)
- Insertar un video video (youtube) que explique o aclare la pregunta con su enlace respectivo (normas Apa)
- Debajo del video realizar un resumen de lo que dice o explica el autor del video.
Desarrollo
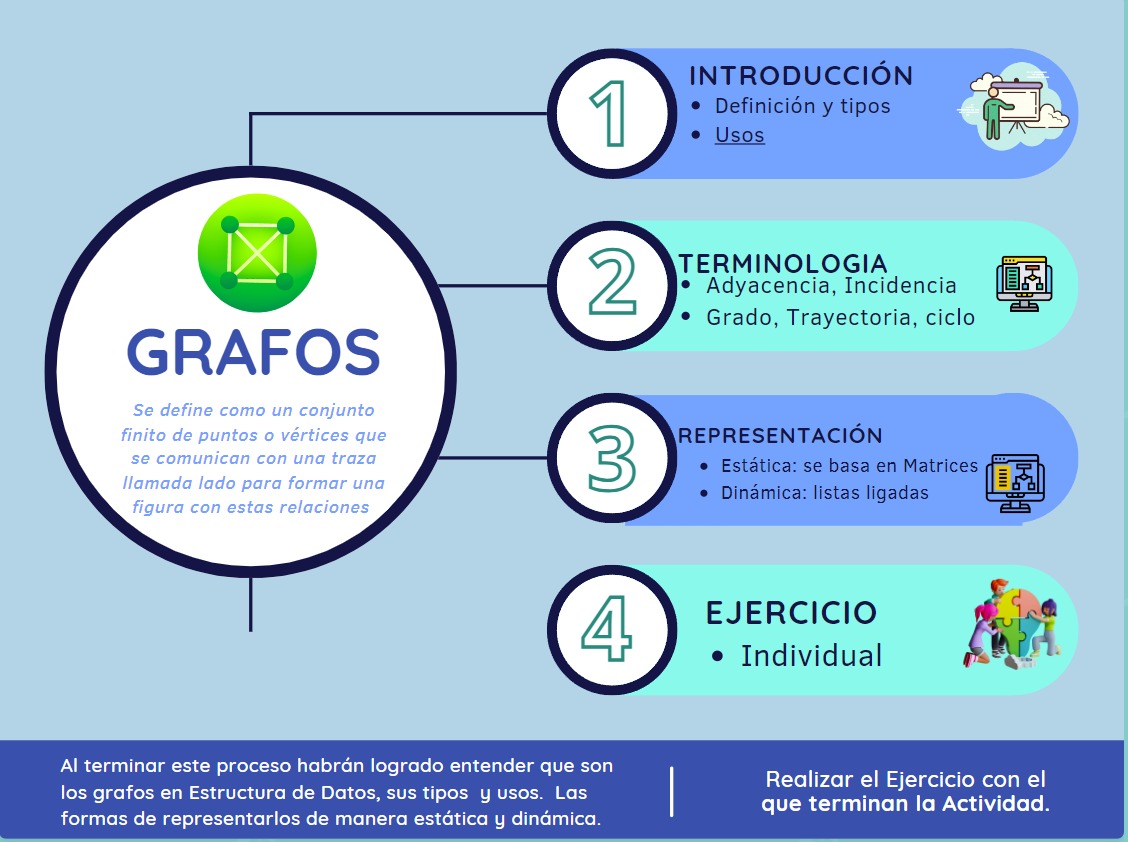
1. Definir que es un grafo
En matemáticas y ciencias de la computación, un grafo (del griego grafos: dibujo, imagen)1 es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto.2Son objeto de estudio de la teoría de grafos.3
Típicamente, un grafo se representa gráficamente como un conjunto de puntos unidos por líneas (aristas o arcos).
Desde un punto de vista práctico, los grafos permiten estudiar las interrelaciones entre unidades que interactúan unas con otras. Por ejemplo, una red de computadoras puede representarse y estudiarse mediante un grafo, en el cual los vértices representan terminales y las aristas representan conexiones (las cuales, a su vez, pueden ser cables o conexiones inalámbricas).
Prácticamente cualquier problema puede representarse mediante un grafo, y su estudio trasciende a las diversas áreas de las ciencias exactas y las ciencias sociales.
colaboradores de Wikipedia. (2024, 31 julio). Grafo. Wikipedia, la Enciclopedia Libre. https://es.wikipedia.org/wiki/Grafo
APORTE PERSONAL: En resumen, un grafo es una forma de representar relaciones entre diferentes elementos, donde los puntos son los elementos (vértices) y las líneas que los conectan son las relaciones (aristas). Esta herramienta es útil para analizar cómo interactúan estos elementos en diversas situaciones, desde redes de computadoras hasta problemas sociales.
El Taller De TD. (2022, 16 julio). Teoría de GRAFOS en INFORMÁTICA: Que es un grafo, Tipos de Grafos, como representarlos y ejemplos [Vídeo]. YouTube. https://www.youtube.com/watch?v=F5Xjpg0-NhM
APORTE DE EL VIDEO : El video de El Taller De TD introduce la teoría de grafos en informática, explicando qué es un grafo y los diferentes tipos que existen, como grafos dirigidos y no dirigidos. Se discuten diversas formas de representación, como matrices y listas de adyacencia, junto con ejemplos prácticos. También se mencionan aplicaciones de los grafos en áreas como redes y algoritmos. El contenido es accesible y ayuda a entender los conceptos fundamentales de esta rama de la informática. En resumen, es una guía útil para iniciarse en la teoría de grafos.
2. ¿Que uso se le dan a los grafos?
Los grafos son utilizados dentro de diversos campos como la ingenier´ıa el´ectrica, qu´ımica, ingenier´ıa industrial, compiladores, sistemas operativos, organizaci´on y recuperaci´on de la informaci´on entre otras disciplinas. Los grafos son estructuras de datos, es decir, tipos de datos abstractos, com´unmente los grafos son utilizados para el modelado de problemas.
Los grafos tienen muchos tipos de aplicaciones, tanto de mapas como aplicaciones matemáticas, como resolver problemas sobre búsqueda de caminos con el menor costo, por ejemplo, la ruta que usará el taxi para llevar a una persona a su destino.
La utilidad y aplicación de los Grafos y Sistemas de Información Geográfica. (s. f.). Delfino.cr. https://delfino.cr/2023/01/la-utilidad-y-aplicacion-de-los-grafos-y-sistemas-de-informacion-geografica<br>
Aporte personal definir con sus propias palabras la pregunta en 5 lineas
Los grafos se utilizan para representar y entender conexiones entre elementos en diversas situaciones cotidianas. Por ejemplo, nos ayudan a encontrar la ruta más corta entre dos lugares, como cuando usamos un GPS. También permiten visualizar relaciones sociales, como quiénes son amigos de quién en una red social. Además, los grafos ayudan a organizar el flujo de información en redes de computadoras o a mejorar búsquedas en internet. En general, los usamos para simplificar y resolver problemas donde las conexiones entre cosas son clave.
https://images-na.ssl-images-amazon.com/images/I/51FeGK0rmGL.png
edX. (2015b, mayo 7). Aplicaciones de la Teoría de Grafos a la Vida Real (I) | UPValenciaX on edX | Course About Video [Vídeo]. YouTube. https://www.youtube.com/watch?v=dP7-gXXXiaM
Resumen Del Video
El video aborda cómo la teoría de grafos se aplica en la vida real. El autor explica que los grafos permiten modelar y resolver problemas cotidianos, como la planificación de rutas, la optimización de redes eléctricas o de transporte, y la conexión entre personas en redes sociales. También se menciona cómo los grafos son fundamentales en la informática y la ciencia de datos, ayudando a organizar información y optimizar procesos. Se destacan ejemplos claros y aplicaciones prácticas en diversas áreas.
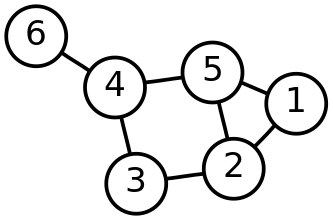
3. ¿Como se pueden clasificar los grafos?
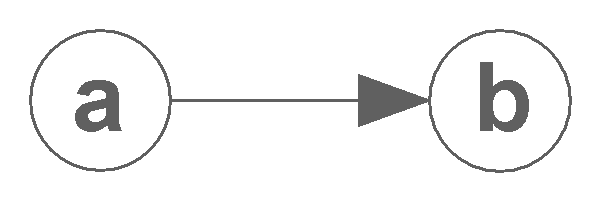
Los grafos dirigidos, también llamados dígrafos, son aquellos en los que las aristas (o arcos) tienen una dirección específica, lo que indica que la conexión entre dos nodos va en un solo sentido. Cada arista es una pareja ordenada de nodos, por lo que si existe una arista de un nodo A hacia un nodo B, esto no implica necesariamente que haya una arista de B hacia A. Estos grafos se usan comúnmente para modelar situaciones donde las relaciones son asimétricas, como en redes de tráfico, flujos de trabajo, o jerarquías.
Por otro lado, los grafos no dirigidos son aquellos en los que las aristas no tienen dirección. Las conexiones entre nodos son bidireccionales, lo que significa que si existe una arista entre el nodo A y el nodo B, se puede ir de A a B y de B a A. Este tipo de grafos se utiliza para modelar relaciones simétricas, como las redes sociales donde dos personas son amigos mutuamente, o en sistemas donde las conexiones no dependen de la dirección.
En ambos casos, los grafos pueden representar estructuras de datos y relaciones de una manera gráfica y fácil de entender, lo que los hace fundamentales en diversas áreas de la informática y la teoría de redes.
Sedgewick, R., & Wayne, K. (2011). Algorithms. Addison-Wesley Professional.
APORTE PERSONAL: Los grafos dirigidos, o dígrafos, tienen aristas con dirección, lo que indica relaciones asimétricas, como en redes de tráfico o jerarquías. En contraste, los grafos no dirigidos permiten conexiones bidireccionales, representando relaciones simétricas, como amistades en redes sociales. Ambos tipos de grafos son útiles para modelar estructuras de datos y relaciones de manera visual. Su representación gráfica facilita el análisis en diversas áreas de la informática y la teoría de redes. En resumen, son herramientas clave para entender interacciones y flujos en diferentes contextos.
Grafo no dirigido
colaboradores de Wikipedia. (2024c, julio 31). Grafo. Wikipedia, la Enciclopedia Libre. https://es.wikipedia.org/wiki/Grafo#/media/Archivo:Kaari_suuntaamaton_graafiteoria.png

Grafo Dirigido
colaboradores de Wikipedia. (2024d, julio 31). Grafo. Wikipedia, la Enciclopedia Libre. https://es.wikipedia.org/wiki/Grafo#/media/Archivo:Kaari_suunnattu_graafiteoria.png
CHOCHY. (2021a, julio 23). Grafo dirigido y no dirigido [Vídeo]. YouTube. https://www.youtube.com/watch?v=IVDX8cGw1CM
Resumen de el video
En el video de CHOCHY se explican las diferencias entre grafos dirigidos y no dirigidos. Se definen los grafos dirigidos como aquellos donde las conexiones tienen una dirección específica, lo que indica relaciones asimétricas. Por otro lado, los grafos no dirigidos permiten conexiones bidireccionales, representando relaciones simétricas. A través de ejemplos visuales, se ilustra cómo cada tipo de grafo se utiliza en diferentes contextos, facilitando la comprensión de sus aplicaciones en informática y teoría de redes.
4. ¿Como se pueden representar los grafos?
Las dos representaciones principales de grafos son las siguientes:
- Matriz de adyacencia (MA): Se utiliza una matriz de tamaño n × n donde las filas y las columnas hacen referencia a los vértices para almacenar en cada casilla la longitud entre cada par de vértices del grafo. La celda MA[i, j] almacena la longitud entre el vértice i y el vértice j. Si su valor es infinito significa que no existe arista entre esos vértices, y MA[i, i] = 0.
Listas de adyacencia
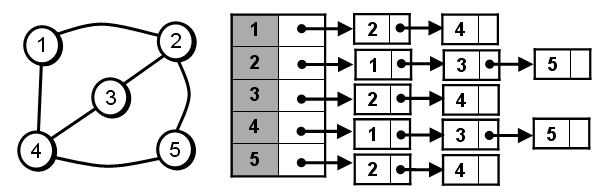
- Lista de adyacencia (LA): Se utiliza un vector de tamaño n (un elemento por cada vértice) donde LA[i] almacena la referencia a una lista de los vértices adyacentes a i. En una red esta lista almacenará también la longitud de la arista que va desde i al vértice adyacente.
colaboradores de Wikipedia. (2024, 31 julio). Grafo. Wikipedia, la Enciclopedia Libre. https://es.wikipedia.org/wiki/Grafo
APORTE PERSONAL: En resumen, hay dos formas principales de representar un grafo: la matriz de adyacencia, que usa una tabla para mostrar las conexiones y distancias entre todos los vértices, y la lista de adyacencia, que utiliza una lista para mostrar solo los vértices cercanos a cada uno. Ambas representaciones ayudan a entender las relaciones en un grafo de manera clara y eficiente.
Imagen Matriz de adyacencia
colaboradores de Wikipedia. (2024, 31 julio). Grafo. Wikipedia, la Enciclopedia Libre. https://es.wikipedia.org/wiki/Grafo#/media/Archivo:Matriz_de_adyacencia.jpg
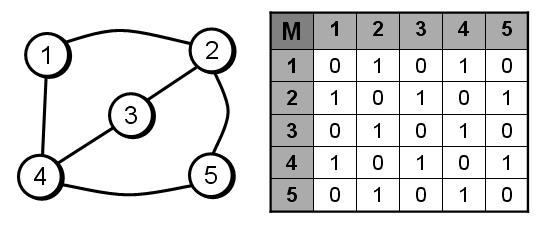
Imagen Listas de adyacencia
colaboradores de Wikipedia. (2024b, julio 31). Grafo. Wikipedia, la Enciclopedia Libre. https://es.wikipedia.org/wiki/Grafo#/media/Archivo:Listas_de_adyacencia.jpg
CHOCHY. (2021, 25 julio). Matriz de adyacencia, matriz de incidencia y lista de adyacencia [Vídeo]. YouTube. https://www.youtube.com/watch?v=lvOQOoMcj5I
APORTE PERSONAL DEL VIDEO: El video de CHOCHY explica las diferentes formas de representar grafos: la matriz de adyacencia, que muestra conexiones y distancias entre todos los vértices; la matriz de incidencia, que relaciona vértices y aristas; y la lista de adyacencia, que detalla solo los vértices conectados a cada nodo. Se analizan sus características, ventajas y desventajas. Estas representaciones son útiles en la teoría de grafos para resolver problemas de interconexión. En resumen, el video ofrece una visión clara sobre cómo manejar y estudiar grafos.
